- Home
- News
- Spotlight on Science
- Hard X-ray spectroscopy...
Hard X-ray spectroscopy with “Newton’s prism”
30-08-2019
Spectrographic imaging with visible light has been known since the invention of Newton’s prism. In the hard X-ray domain, this approach is hampered by the constraints of X-ray optics. Now, the principles of spectrographic imaging have been applied to hard X-ray spectroscopy improving the energy resolution by an order of magnitude without significant loss in intensity. In phonon spectroscopy, the technique has revealed anomalous soft atomic dynamics in α-iron, a previously unknown phenomenon in an extensively-studied system.
In hard X-ray spectroscopy, the monochromators and analysers work as narrow-band filters, eliminating photons of all energies other than the desired ones. Within this approach, any attempt to narrow the energy bandwidths for improving the energy resolution inevitably reduces the intensity.
A breakthrough solution to this problem would be to complement hard X-ray spectroscopy by the principles of spectrographic imaging, widely used in a vast spectral range from infrared radiation to soft X-rays. A spectrograph keeps radiation components of all energies, dispersing the “colours” spatially. Consequently, the energy resolution is provided by selecting distinct components in space, whereas the availability of all these components keeps the entire intensity.
For visible light, the concept of spectrographic imaging – dispersion of radiation components with various energies in space – has been known since Newton’s time. But for hard X-rays, optical prisms and conventional diffraction gratings are not efficient. Nevertheless, the principles of the angular dispersion of hard X-rays are known [1-3]. They rely on the angular dispersion of X-rays in Bragg diffraction by asymmetrically cut crystals. Combined with focusing optics, this results in dispersing X-rays of different energies in space [1-4], and using the entire beam in all spatial coordinates in parallel, which preserves the total intensity. Optical schemes for hard X-ray spectrographs have already been studied [3] and demonstrated [2]. Such a scheme has now been applied to hard X-ray spectroscopy in recent experiments at the ESRF.
Spectrographic hard X-ray imaging was demonstrated at beamline ID18 in measurements of the density of phonon states by nuclear inelastic scattering using 14.4125 keV photons corresponding to the energy of the nuclear resonance of the 57Fe isotope.
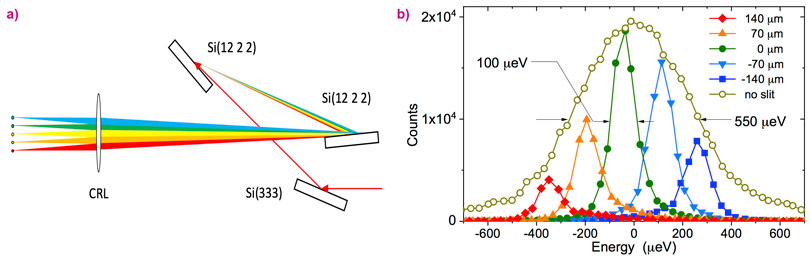
The key elements of the hard X-ray spectrograph are shown in Figure 1a. The dispersion is provided by the second and the third silicon crystals in the highly asymmetric (12 2 2) reflections. The first silicon crystal is used to maintain the exit beam in the horizontal direction approximately, and the downstream multilayer mirror (not shown) assures this precisely. The compound refractive lens focuses radiation components with different energies to different vertical coordinates, providing the spatial dispersion. Since the radiation components of various energies are separated in space, the scheme allows for measurements of the density of states with several identical (or different) samples in parallel, benefiting from the improved energy resolution and conserved intensity.
Figure 1b shows the energy distributions of X-ray components selected by a 20 μm-wide slit at five indicated vertical positions, and the energy distribution of an entire beam measured without the slit. The measurement without the slit defines the spectral window of the spectrograph. With a sufficiently small slit (in this case – 20 mm), the measurements give the energy resolution of the spectrograph. Figure 1b shows that the spectral window of the spectrograph is 550 meV, and the energy resolution is about 100 meV. This compares well with the best resolution of Raman spectroscopy. Furthermore, it is about an order of magnitude better than the typical resolution of presently employed hard X-ray inelastic scattering spectrometers. For nuclear inelastic scattering, however, improving the energy resolution is certainly easier as the method does not require energy analysers and momentum resolution.
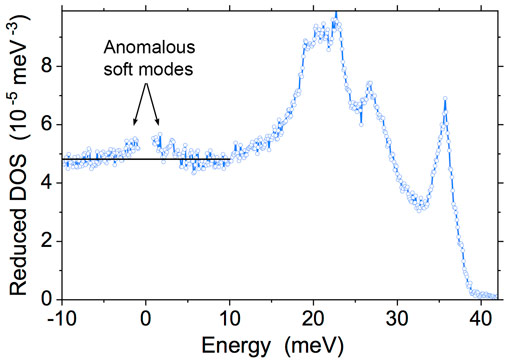
Figure 2 demonstrates spectrographic imaging in the measurement of the density of phonon states in α-iron. The energy resolution is improved by an order of magnitude and reveals anomalous soft modes (Figure 2), a previously unknown phenomenon of this already extensively studied system. Additional data show that this phenomenon is intrinsic to an ideal lattice of α-iron, and cannot be attributed to possible imperfections such as impurities, grain boundaries, dislocations, texture, and magnetic domain walls. Plausibly, the observed anomalous dynamics is related to anharmonic effects and/or magneto-elastic waves.
Principal publication and authors
Hard-X-ray spectroscopy with a spectrographic approach, A.I. Chumakov (a), Yu. Shvyd’ko (b), I. Sergueev (c), D. Bessas (a), R. Rüffer (a), Physical Review Letters 123, 097402 (2019); DOI: 10.1103/PhysRevLett.123.097402.
(a) ESRF
(d) Advanved Photon Source, Argonne National Laboratory, Argonne, IL (USA)
(c) DESY, Hamburg (Germany)
References
[1] X-ray Optics — High-Energy-Resolution Applications, Y. Shvyd'ko, vol. 98 of Optical Sciences (Springer, Berlin, 2004).
[2] Hard-X-ray spectrograph with resolution beyond 100 meV, Y. Shvyd'ko, S. Stoupin, K. Mundboth, and J. Kim, Phys. Rev. A 87, 043835 (2013).
[3] Theory of angular dispersive, imaging hard X-ray spectrographs, Y. Shvyd'ko, Phys. Rev. A 91, 053817 (2015).
[4] Wave theory of focusing monochromator of synchrotron radiation, V.G. Kohn, A.I. Chumakov, and R. Rüffer, J. Synchrotron Radiation 16, 635 (2009).